An Irrational hybrid in an Analogue-Digital world?

Nature’s four great irrationals \delta, \phi,  \pi and e are encoded in much of what we describe as physical reality. One way to demarcate them is according to their discrete or continuous (analytic) origins. A fifth irrational, the lesser-known Euler-Mascheroni constant, \gamma traverses the analogue functions of the analytic (mathematical) modeller and the apparent discrete reality of the physical world. It appears in physicist’s regularisation programs of quantum field theory of electrodynamics, that coarsen an otherwise too finely-tuned view of the world.

We consider in the following whether or not \gamma  deserves its place in Nature’s hall of fame. Consider the big four. The Digitals of sequencing and non-linear growth:

  • \delta –Feigenbaum’s number 4.669201609…, that universal constant of chaos theory being the limiting value characterising the velocity of period-doubling, the ratio of the intervals between bifurcation points of dynamical system approaching chaotic behaviour (planetmath.org).
  • \phi -golden ratio (√5-1)/2=1.618033988…that irrational limit to which ratios of successive numbers in the iterative Fibonacci sequence 1,1,2,3,5,8,13,.. tends. The ratio is characterised by  log spiral and the non-Markovian (see below) nature of sequential growth.

The Analogues of trigonometry and analysis:

  • \pi 3.14159265359.. that ratio of circumference over diameter that reflects the flatness of the space in which a locus of points a fixed distance from a central point scribe. Alternatively the area that scribed circle (x^2 +y^2=r^2) encapsulates if its radius, r is one unit.
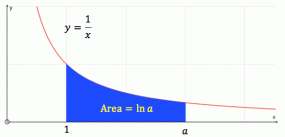
  • e- Euler’s number, 2.71828182845.. that number beyond x=1 (on the real number line) at which the definite integral (area) under the hyperbola y=1/x is one unit.That is when the domain of function is (1,a=e) as in the graph below,

To these four irrationals should wee add to Nature’s true “Natural numbers” the “hybrid” (as yet to be confirmed definitively irrational):

  •  \gamma ≈0.5772156649…, Euler-Mascheroni constant.

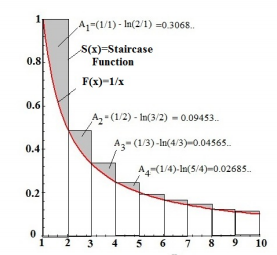
Logarithmically accumulating Harmonic Series

Whereas \ln(n) is the limit of the area of the analytic hyperbola 1/x as we extend a in the graph above to infinity, our digital harmonic series,

\sum_{k=1}^\infty\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+...

cumulatively grows”logarithmically’ slowly. The Euler-Mascheroni constant,  ɣ  is the finite difference between this accumulating divergent Harmonic series and the divergent hyperbola, \gamma=\lim_{n\to\infty}(-\ln n+\sum^n_{k=1}\frac{1}{k}) being the grey area in the graph below.
 The difference between the two series being, \sum_{k=0}^n \frac{1}{2n(n+1)}-\ln(\frac{n+1}{n})<\gamma<\int_{x=2}^\infty (\frac{1}{x}-\frac{1}{x-1})dx fixing its value to be between 0.4851 and the limit of the convergent alternating harmonic series, 0.485099..<\gamma<\ln(2)=0.693147.. Rather than trying to pin down the number by deploying  \Psi and \Gamma functions, which is done ably here (mae.ufl.edu), we merely take a nod at the harmonic series’ close acquaintances, both mathematical and physical.

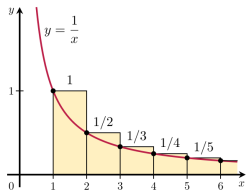
Alternating Harmonic Series limit of ln(2) and Decay Modelling

Unlike its corpulent divergent brother, the alternating harmonic series,

1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+...+ \frac{(-1)^{n+1}}{n}+...

converges to ln(2), which in itself is the area under the hyperbola defined between the domain interval of [1, 2]. This \ln(2) limiting value is a number familiar to those acquainted with exponential radioactive decay.

The deterministic model for a decaying (aggregate) set of discrete elements, N(t), governed by quantum selection rules, says that the mean lifetime an element remains in the set relates to the decay rate, \lambda (characteristic) of the sample, N(t)=N_0e^{-\lambda t}. The time required for the decaying quantity to fall to one half of its initial value is the ratio of this limit to decay rate, t_{1/2}=\frac{\ln(2)}{\lambda}. When this expression is inserted in the exponential equation above we move from base e to base 2,  N(t)=N_02^{-t/t_{1/2}}.

The statistics of this exponential decay can be derived using a stochastic Markov chain process, that satisfies the (“memory-less“) property that predictions for the future of the process can be based solely on its present state, ignoring the process’s full history.
Unlike the memory-full(er) growth determined by golden ratio \phi, the Euler-Mascheroni constant \gamma characterises radioactive decay that retains no memory of the history that delivered the aggregate to its present unstable stochastic state. Rather than associate Euler’s daughter, e to the grandaughtering of decay, perhaps it is more appropriate to consider such spontaneous processes as governed by Euler’s illegitimate son, \gamma .
We may summarise Nature’s irrationals then according to the following:
  • \pi and  e  embody the Reductionists‘ principle of describing the scattering of light (electromagnetic waves) through homogeneous solids by sets of interacting linear trigonometric functions;
  • ϕ, ẟ encode the complex non-linear dynamics inherent within interacting systems involving non-homogenous condensed matter such as gases and fluids as modelled for example by the Navier-Stokes equations;
  • ɣ  traverses the regime between these memory-less and memory-full processes: between the analogue functions of the mathematical analytic model and the discrete chaotic reality of a physical world of dynamically interacting systems.

Mascheroni constant and Quantized Field theories

In theories of Quantised fields, Renormalization is the process of subtracting counter terms at each order of the “perturbation” (about the linearised) theory. Regularization is the modification of the theory at (shorter) distance (“cutoff”) scales so that the theory becomes well-defined (UMD physics). A “regulator” is a process which renders finite, a momentum integral which is superficially divergent. The Euler-Mascheroni constant, γ appears in the finite part of the integral and to have no apparent physical significance beyond being merely an “artefact” of a coarse-graining subtraction scheme to counter divergences arising from deploying otherwise analogue idealised functions.

A geogebra applet is here, https://www.geogebra.org/m/q2veq4v8